Question

I need help please. Thanks!

Answer 1

A

Explanation:

We are given the function f and its derivative, given by:

`f^\prime(x)=x^2-a^2=(x-a)(x+a)`

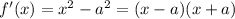
Remember that f(x) is decreasing when f'(x) < 0.

And f(x) is increasing when f'(x) > 0.

Firstly, determining our zeros for f'(x), we see that:

`0=(x-a)(x+a)\Rightarrow x=a, -a`

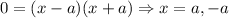
Since a is a (non-zero) positive constant, -a is negative.

We can create the following number line:

<-----(-a)-----0-----(a)----->

Next, we will test values to the left of -a by using (-a - 1). So:

`f^\prime(-a-1)=(-a-1-a)(-a-1+a)=(-2a-1)(-1)=2a+1`

Since a is a positive constant, (2a + 1) will be positive as well.

So, since f'(x) > 0 for x < -a, f(x) increases for all x < -a.

To test values between -a and a, we can use 0. Hence:

`f^\prime(0)=(0-a)(0+a)=-a^2`

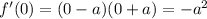
This will always be negative.

So, since f'(x) < 0 for -a < x < a, f(x) decreases for all -a < x < a.

Lasting, we can test all values greater than a by using (a + 1). So:

`f^\prime(a+1)=(a+1-a)(a+1+a)=(1)(2a+1)=2a+1`

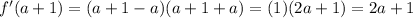
Again, since a > 0, (2a + 1) will always be positive.

So, since f'(x) > 0 for x > a, f(x) increases for all x > a.

The answer choices ask for the domain for which f(x) is decreasing.

f(x) is decreasing for -a < x < a since f'(x) < 0 for -a < x < a.

So, the correct answer is A.