Question

Given the function f(x) = x2 and k = 3, which of the following represents the graph becoming more narrow? A. f(x)+k

B. kf(x)
C. f(x+k)
D. f(x-k)

Answer 1

The following which represents the graph becoming more narrow is:

B. kf(x)

Explanation:

We are given a parent function f(x) as:

`f(x)=x^2`

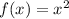
and k=3

Now, we know that the transformation of the type:

f(x)+k

shifts the graph of the function k units upward while there is no change in the shape of graph.

Similarly the transformation f(x+k) and f(x-k) shifts the graph of the original function k units to the left and k units to the right but odes not change the shape of the function.

Hence, the answer is:

B. kf(x)

Since, the transformation is a vertical compression and the graph becomes more narrow.

Answer 2

The only type of transformation that can make a graph more narrow/wide is a scaling transformation. A scaling transformation involves a multiple factor. The answer to your question is B. I hope that this is the answer that you were looking for and it has helped you.