Question

A point of the form 25 +bi is 37 units from 13 – 31i. What is the value of b?

Answer 1

Hello,

Here is an analytic method.
Equation of the circle of center C(13,-31) and radius 37:

(x-13)²+(y+31)²=37²
x=25
We are going to calculate y

(25-13)²+(y+31)²=1369
==>(y+31)²=35²
==>(y=4 or y=-66)

So b=4 or b=-66

Answer 2

The value of b is: 4 and -66

Explanation:

We are given distance between two points i.e. 25+bi and 13-31i as: 37 units.

We know that the point 25+bi is given in coordinate plane as: (25,b)

and 13-31i is given in coordinate plane as: (13,-31)

Since, any complex number is expressed in the form z=x+iy

Now we know that the distance between two points (a,b) and (c,d) is given by:

`Distance=√((c-a)^2+(d-b)^2)`

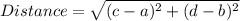
Here we have:

Distance=37 units.

(a,b)=(25,b) and (c,d)=(13,-31)

Hence, we have:

`37=√((13-25)^2+(-31-b)^2)\\\\\\37=√(12^2+(31+b)^2)\\\\\\37=√(144+(31+b)^2)`

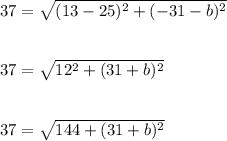
Now on squaring both side we obtain:

`1369=144+(31+b)^2\\\\\\1369-144=(31+b)^2\\\\\\(31+b)^2=1225\\\\\\(31+b)^2=(35)^2`

on taking square root both side we obtain:

`31+b=\pm 35\\\\i.e.\\\\\\b=35-31\ and\ b=-35-31=-66\\\\\\i.e.\ b=4\ and\ b=-66`

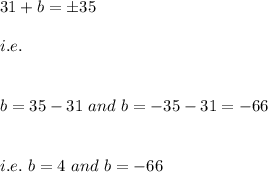
Hence, the value of b is: 4 and -66