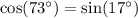At any right angle, the sum of the 2 acute angles is 90 degrees
Then the 2 acute angles are complementary
sin one of the angle = cos the other angle
cos one of the angle = sin the other angle
From the figure, we can see
Triangle UVT is a right angle at V
Then v is the hypotenuse, u and t are the legs od the right angle
Now, let us answer the questions
Part (1):
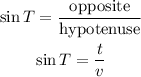
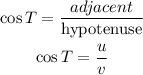

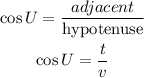
Part (2):
Since
 complementary
complementary
Part (3):
The correct statements are

Part (4):
Since cos a= sin b, then
a + b = 90 degrees
To find the missing angle subtract 73 from 90
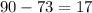
Then the answer is