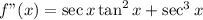Question

Find the second derivative of f(x)=sec(x).

Answer 1

Answer:
`f`

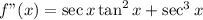
Explanation:

The given function :
`f(x)=\sec x`

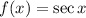
First we find the first derivative of the function, so differentiate both sides , with respect to x, we get

`f'(x)=\sec x\tan x`

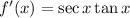
Now, to find the second derivative, we differentiate again it with respect to x, we get

`f`

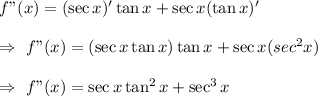
Hence, the second derivative of
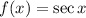`f(x)=\sec x` is
`f`

Answer 2

The derivative of sec x is equal to sec x tan x. The derivative of the first derivative can be determined using the rule of products. The derivative is equal to sec x sec^2 x + tan x * sec x tan x. The simplified answer is sec^3 x + sec^2 x tan x equal to sec^2 x ( sec x + tanx )