Question

Hello! I need help completing this problem. A picture will be included. Thank you so much!

Answer 1

2.91 seconds

Step-by-step explanation

The equation represents the height of the ball from the ground. To find how long does it take to hit the ground, we have to solve the equation when h = 0,

`197-21t-16t^2=0`

Using the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case, the variable is t and the coefficients are a = -16, b = -21, and c = 197,

`t=\frac{-(-21)\pm\sqrt[]{(-21)^2-4\cdot(-16)\cdot197}}{2\cdot(-16)}=\frac{21\pm\sqrt[]{441+12608}}{-32}=\frac{21\pm\sqrt[]{13049}}{-32}\approx(21\pm114.23)/(-32)`

Note that we have two results for t,

`\begin{gathered} t_1=(21-114.23)/(-32)=(-93.23)/(-32)=2.91 \\ \\ t_2=(21+114.23)/(-32)=(135.23)/(-32)=-4.23 \end{gathered}`

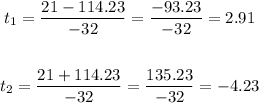
However, one of these results is positive and the other is negative. To decide whether they are valid or not, we have to remember what the variable t represents.

In this case, t represents time and time can't be negative - negative time would represent the time before the ball was thrown.

Hence, the ball hits the ground 2.91 seconds after being thrown.