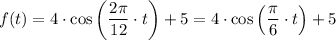Question

In Panama City in January, high tide was at midnight. The water level at high tide was 9 feet and 1 foot at low tide. Assuming the next high tide is exactly 12 hours later and that the height of the water can be modeled by a cosine curve, find an equation for water level in January for Panama City as a function of time (t).

Answer 1

h(t) = a*cos((2pi/P)*t) + b,

a = amplitude of motion,
P = period

b = vertical displacement.

so a = [max. height - {min. height}]/2 =[9 - 1]/2 = 4,

b = [{max. height} +{min. height}]/2 = (9 + 1) / 2 = 5.

As P = 12 hours
so
h(t) = 4*cos[(2pi/12)*t] + 5 = 4*cos((pi/6)*t) + 5 is the required equation
hope it helps

Answer 2

`f(t)=4\cdot \cos\left((\pi)/(6)\cdot t\right) + 5`

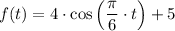
Explanation:

As it is a fluctuating scenario, where the value repeats itself after some time, it must be represented by periodic function.

As the value at the beginning is a non zero value, we should use a Cosine function.

The general cosine function is,

`f(t) = a\cdot \cos\left((2\pi)/(p)\cdot t\right) + b`

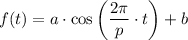
where,

a = amplitude of motion,

p = period ,

b = vertical displacement.

The water level at high tide was 9 feet and 1 foot at low tide. So,

`a=\frac{\text{Max height - Min height}}{2}=(9-1)/(2)=(8)/(2)=4`

`b=\frac{\text{Max height + Min height}}{2}=(9+1)/(2)=(10)/(2)=5`

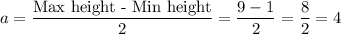
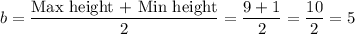
The next high tide is exactly 12 hours later. So period or p = 12

Putting all the values,

`f(t) = 4\cdot \cos\left((2\pi)/(12)\cdot t\right) + 5=4\cdot \cos\left((\pi)/(6)\cdot t\right) + 5`