Question

The area of a square is decreasing at a rate of 89 square meters per minute. At the time when the side length of the square is 7, what is the rate of change of the perimeter of the square? Round your answer to three decimal places (if necessary).

Answer 1

Question: We want to know the value of the rate of change of the perimiter of the square:

`(dP)/(dt)=\text{?}`

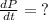
1) We know that the perimiter of a square is:

`P=4L`

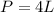
We find the rate of change of the perimiter (dL/dt) taking its derivative:

`(dP)/(dt)=4(dL)/(dt)`

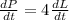
From the last equation we see that we need the rate of change of the side (dL/dt) in order to calculate the rate of change of the perimeter (dP/dt).

2) Now, according to the question the area of the square is changing at a rate:

`(dA)/(dt)=-89(m^2)/(\min)`

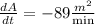
We know that the area of square is:

`A=L^2`

We can calculate the rate of change of the side (dL/dt) taking the derivative of the area:

`(dA)/(dt)=2L\cdot(dL)/(dt)`

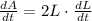
Now, taking the data of the rate of change of the area and the last formula we see that:

`\begin{gathered} 2L\cdot(dL)/(dt)=-89(m^2)/(\min) \\ (dL)/(dt)=-(89)/(2L)(m^2)/(\min) \end{gathered}`

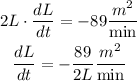
3) Replacing the value of the rate of change of the side (dL/dt) in the formula of the rate of change of the perimeter (dP/dt) we find that:

`(dP)/(dt)=4(dL)/(dt)=-4\cdot(89)/(2L)\cdot(m^2)/(\min)`

Finally, replacing the value of the side L = 7 m we find that te rate of change of the perimeter is:

`(dP)/(dt)=-4\cdot(89)/(2\cdot7m)\cdot(m^2)/(\min)\cong-25.429\frac{m^{}}{\min}`

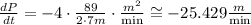
So the perimeter of the square is decreasing at a rate of 25.429 m/min.