Let
x-------> the length side of the equilateral triangle
y-------> the length side of the square
we know that
The sum of the perimeters of an equilateral triangle and a square is
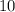
Perimeter of triangle is equal to

Perimeter of the square is equal to
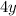
so
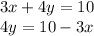
 ------> equation
------> equation

Find the area of equilateral triangle
Applying the law of sines
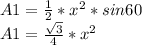
Find the area of the square
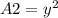
Fin the total area
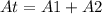
 ----> equation
----> equation
Substitute equation
 in equation
in equation
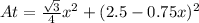
Using a graph tool
see the attached figure
we know that
the vertex of the graph is the point with the minimum total area
the vertex of the graph is the point
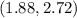
that means that
for
 the total area is equal to
the total area is equal to
 (is the minimum total area)
(is the minimum total area)
find the value of y
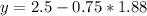
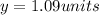
therefore
the answer is
the length side of the equilateral triangle is equal to
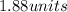
the length side of the square is equal to
