Question

I have attached a photo of the example and the question.

Answer 1

1) According to the problem, each kiddie ride ticket costs 3 tokens. Therefore, for 5 kiddie rides, the total cost for one person is 3*5=15. However, if Akira is also on the kiddie ride the same five times, the total cost is 30

Thus, the inequality is

`5t+3(10)\le50`

Solving for t,

`\begin{gathered} \Rightarrow5t+30\le50 \\ \Rightarrow5t+30-30\le50-30 \\ \Rightarrow5t\le20 \\ \Rightarrow(5t)/(5)\le(20)/(5) \\ \Rightarrow t\le4 \end{gathered}`

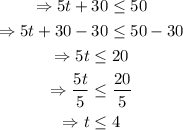
Akira could go on 0, 1, 2, 3, or 4 thrill rides.

2) Let x be the number of additional boxes; therefore, the inequality that models the problem is

`750x+750\cdot18\le20000`

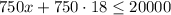
Solving for x,

`\begin{gathered} \Rightarrow750x+13500\le20000 \\ \Rightarrow750x+13500-13500\le20000-13500 \\ \Rightarrow750x\le6500 \\ \Rightarrow(750x)/(750)\le(6500)/(750) \\ \Rightarrow x\le(26)/(3) \\ \Rightarrow x\le8.6667 \end{gathered}`

Therefore, one can fit 8 extra boxes at most.