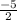Question

Solve the system of equations:

y = 2x^2 - 3
y = 3x - 1

Answer 1

for x=2 , y=5 and x=
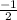`(-1)/(2)` , y=
`(-5)/(2)`

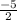
Explanation:

Given : y = 2x² - 3 and y = 3x - 1.

To find : Solve the system of equations.

Solution : We have given that

y =2x² - 3 ---------(equation number 1)

y = 3x - 1. ----------(equation number 2)

Substitute the equation 1 in equation 2

2x² -3 = 3x -1

On subtracting both side by 3x.

2x² -3 -3x =3x -1 -3x

2x² -3 -3x = -1

On adding both side by 1.

2x² -3 -3x +1 = -1 +1

2x² -3x -2 = 0

On factoring

2x² -4x +x -2 = 0

Taking common 2x from fisrt two term and 1 from last two term.

2x(x-2) +1 (x-2) =0

On grouping

(2x+1) (x-2) =0

2x+1 =0

x=
`(-1)/(2)`

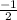
x-2 =0

x=2

Plugging x=2 in second term.

y= 3x-1

y=3*2-1

y=5

Plugging x= - 1/2 in second term.

y= 3x-1

y=3(
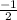`(-1)/(2)`) -1

y=
`(-5)/(2)`

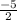
Therefore , for x=2 , y=5 and x=
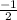`(-1)/(2)` , y=
`(-5)/(2)`

Answer 2

Given:

y = 2x^2 - 3
y = 3x - 1

Equating both:

2x^2 - 3 = 3x - 1
2x^2 - 3x - 3 + 1 = 0
2x^2 - 3x - 2 = 0
(x - 2)(x + 1/2) = 0

Substituting both values of x, the possible values of y are:

y = 5 = -5/2

Therefore, the possible solutions are as follows:

x = 2, y = 5
x = -1/2, y = -5/2