Question

In the rhombus, m∠1 = 18x, m∠2 = x + y, and m∠3 = 30z. Find the value of each variable. The diagram is not drawn to scale. (image attached)thank you ! :)

Answer 1

Explanation:

Answer 2

A rhombus is a type of parallelogram, and what distinguishes its shape is that all four of its sides are congruent.

One of the properties of a rhombus is the fact that diagonals are perpendicular. In another words, the given three measures all measure 90º.

Using this information for m∠1, we can determinate the value of x.

`m\angle1=90^o\implies18x=90\implies x=(90)/(18)=5`

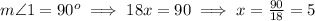
Now that we have the value for x and the measure of ∠2 we can determinate y.

`\begin{gathered} m\angle2=x+y \\ 90=(5)+y \\ y=85 \end{gathered}`

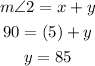
We have the measure of ∠3, therefore, we can determinate z.

`30z=90\implies z=(90)/(30)=3`

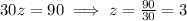
The values of each variable are

`x=5,\:y=85,\:z=3`