Answer:
Given the equation:
 .....[1]
.....[1]
Solve for x;
Divide both sides by -4 in [1]; we get;
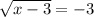
Squaring both the sides we get;
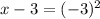
or

Add 3 both sides we get;
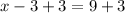
Simplify:
x= 12
Extraneous solution states that it is a root of a transformed equation that is not a root of the original equation because it was excluded from the domain of the original equation.
Substitute x= 12 in [1]


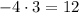
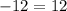 False.
False.
Therefore, the value of x is 12 and it is an extraneous solution.