Question

Determine whether the lines 25x+15y=9 and 5y=3x- 10 are parallel, perpendicular or coincideDarallel

Answer 1

Let's begin by listing out the information given to us:

`\begin{gathered} 25x+15y=9----1 \\ 5y=3x-10-----2 \end{gathered}`

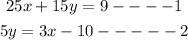
To know this, we will calculate the slope:

`\begin{gathered} y=mx+b \\ where\colon m=slope \\ 25x+15y=9 \\ We\text{ will make variable y the subject of the formula},\text{ subtract 25x from both sides} \\ 25x-25x+15y=-25x+9 \\ 15y=-25x+9 \\ \text{divide through by 15 (the coefficient of y)} \\ (15y)/(15)=-(25)/(15)x+(9)/(15) \\ y=-(5)/(3)x+(3)/(5);m=-(5)/(3) \\ \\ 5y=3x-10 \\ \text{divide through by 5 (the coefficient of y)} \\ (5y)/(5)=(3)/(5)x-(10)/(5) \\ y=(3)/(5)x-2;m=(3)/(5) \end{gathered}`

We will see that the slopes of the two equations are a negative reciprocal (-1/m) of one another. This therefore informs us that the lines are parallel to one another