How many real zeros will x^2+19=8x+3

Question

asked Sep 21, 2022 187k views

1 Answer

Skeept · Answer 1 · 2022-09-26T23:27:32+0000

Answer:

The solution to the quadratic equation is:

x=4

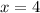
Thus, there will be one real zero.

Explanation:

Given the equation

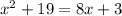
x^2+19=8x+3

Subtract 19 from both sides

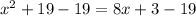
x^2+19-19=8x+3-19

Simplify

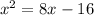
x^2=8x-16

Subtract 8x from both sides

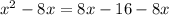
x^2-8x=8x-16-8x

Simplify

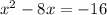
x^2-8x=-16

Add (-4)² to both sides

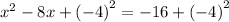
$x^2-8x+\left(-4\right)^2=-16+\left(-4\right)^2$

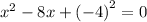
$x^2-8x+\left(-4\right)^2=0$

Apply perfect square rule: (a-b)² = a² - 2ab + b²

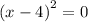$\left(x-4\right)^2=0$ ∵
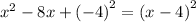
$x^2-8x+\left(-4\right)^2=\left(x-4\right)^2$

so solve

x-4=0

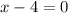
Add 4 to both sides

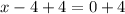
x-4+4=0+4

Simplifying

x=4

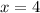
Therefore, the solution to the quadratic equation is:

x=4

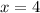
Thus, there will be one real zero.