Question

EFG and ∠GFH are a linear​ pair, m∠EFG 3n+23​, and m∠GFH 4n+17. What are m∠EFG and m∠​GFH?

Answer 1

m∠EFG = 3n + 23
m∠GFH = 4n + 17

m∠EFG + m∠GFH = 180
(3n + 23) + (4n + 17) = 180
(3n + 4n) + (23 + 17) = 180
7n + 40 = 180
- 40 - 40
7n = 140
7 7
n = 20

m∠EFG = 3n + 23
m∠EFG = 3(20) + 23
m∠EFG = 60 + 23
m∠EFG = 83

m∠GFH = 4n + 17
m∠GFH = 4(20) + 17
m∠GFH = 80 + 17
m∠GFH = 97

Answer 2

Answer: m∠EFG=83°

m∠GFH =97°

Explanation:

Given : ∠EFG and ∠GFH are a linear​ pair.

m∠EFG=3n+23​, and m∠GFH=4n+17.

We know that linear pair of angles added up to 180 degrees.

i.e
`\angle{EFG}+\angle{GFH}=180^(\circ)`

`\Rightarrow\ 3n+23+4n+17=180\\\\\Rightarrow\ 7n+40=180\\\\\Rightarrow\ 7n=180-40\\\\\Rightarrow\ 7n=140\\\\\Rightarrow\ n=(140)/(7)=20`

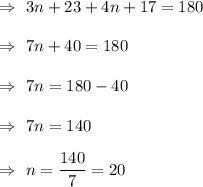
Now, m∠EFG=(3n+23)°= (3(20)+23)°=(60+23)°=83°

m∠GFH =(4n+17)°=(4(20)+17)°=(80+17)°=97°