Answer:
Hence,
 is not defined for odd multiples of
is not defined for odd multiples of
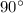 .
.
Explanation:
We are given that
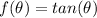
We have to find the value of theta for which

We know that when
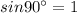
and
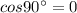
Then
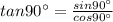
Substituting values
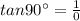
 is not defined .
is not defined .
If we take
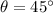

Hence,
 is defined for odd multiples of
is defined for odd multiples of
 .
.
If we take
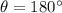
Then
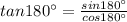
We know that
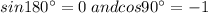
Therefore.

We know that 180 is even multiple of 90 and even multiple of 45 .Hence, we can say
 is no defined for odd multiples of 90
is no defined for odd multiples of 90
because
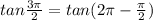
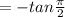
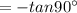
=not defined.
Hence,
 is not defined for odd multiples of
is not defined for odd multiples of
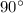 .
.