Question

Functions f(x) and g(x) are shown below. f(x) = x2. . g(x) = x2 - 8x + 16. In which direction and by how many units should f(x) be shifted to obtain g(x)? A. Left by 4 units

B. Right by 4 units
C. Left by 8 units
D. Right by 8 units

Answer 1

Option B is correct.

Right by 4 units

Explanation:

Given the function :
`f(x) = x^2` and
`g(x)=x^2-8x+16`

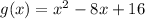
Horizontal shift: Given a function f , a new function g(x) = f(x-h) , where h is constant is a horizontal shift of the function f.

* If h is positive, the graph will shift right.

* if h is negative, then the graph will shift left.

`g(x)=x^2-8x+16`

`x^2 -4x-4x +16`

`x(x-4)-4(x-4)`

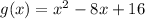
Take (x-4) common;

`(x-4)(x-4)` or

`(x-4)^2` [ Using
`a^m \cdot a^n = a^(m+n)` ]

Then, the function becomes;

g(x) =
`(x-4)^2`

A function g(x)=
`(x-4)^2` , this function comes from the parent function
`f(x) = x^2` with constant 4 subtract to it, this gives the horizontal shift right 4 units. so, take the parent function and shift 4 units right.

Therefore, a function f(x) be shifted right by 4 unit to obtain g(x)

Answer 2

The original function is given by:

`f (x) = x ^ 2`
We apply the following transformation:
Horizontal displacements:
Suppose k> 0
To move the graph k units to the right, we must graph f (x-k)
Applying the transformation for k = 4 we have:

`g (x) = f (x-4) g (x) = (x-4) ^ 2 g (x) = x ^ 2 - 8x + 16`
Answer:
B. Right by 4 units