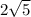Question

How would you solve this? help.

Answer 1

Center: (3,3)

Radius:
`2√(5)`

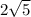
Explanation:

Midpoint and Distance Between two Points

Given two points A(x1,y1) and B(x2,y2), the midpoint M(xm,ym) between A and B has the following coordinates:

`\displaystyle x_m=(x_1+x_2)/(2)`

`\displaystyle y_m=(y_1+y_2)/(2)`

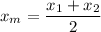
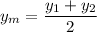
The distance between both points is given by:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

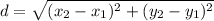
Point (5,7) is the center of circle A, and point (1,-1) is the center of the circle B. Given both points belong to circle C, the center of C must be the midpoint from A to B:

`\displaystyle x_m=(5+1)/(2)=(6)/(2)=3`

`\displaystyle y_m=(7-1)/(2)=(6)/(2)=3`

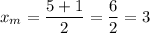
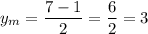
Center of circle C: (3,3)

The radius of C is half the distance between A and B:

`d=√((1-5)^2+(-1-7)^2)`

`d=√(16+64)=√(80)=√(16*5)=4√(5)`

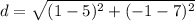
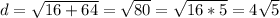
The radius of C is d/2:

`r =4√(5)/2 = 2√(5)`

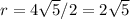
Center: (3,3)

Radius:
`2√(5)`