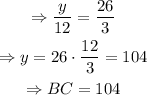Suppose that triangles ABC and DFE are similar. Therefore, the ratio between their corresponding sides is constant. Let x and y be
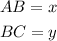
Then,
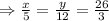
Triangle DFE is impossible, the lengths of its sides are impossible to construct in such a manner that the result is a right triangle whose hypotenuse is 3. DFE is an impossible triangle, the hypotenuse of a right triangle is always its largest side.
However, we can algebraically find x and y, although it would not make any sense geometrically speaking.

Solving for x,
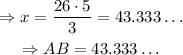
Similarly, solving for y,