Question

Line FG contains points F (3,7) and G (-4,-5) line HI contains points (-1,0) and I (4,6) lines FG and HI are. ?

a. parellel
b. perpendicular
c. neither

Answer 1

FG : (3,7)(-4,-5)
slope = (-5 - 7) / (-4-3) = -12/-7 = 12/7

y = mx + b
slope(m) = 12/7
(3,7)...x = 3 and y = 7
now we sub, we r looking for b, the y int
7 = 12/7(3) + b
7 = 36/7 + b
7- 36/7 = b
49/7 - 36/7 = b
13/7 = b
so ur equation is : y = 12/7 + 13/7.....slope = 12/7, y int = 13/7

HI : (-1,0)(4,6)
slope = (6 - 0) / (4 - (-1) = 6/5

no need to go any farther.....these lines have different slopes...and their not negative reciprocals....so there will be one solution. Answer is : neither.

Answer 2

Option C neither is the answer.

Explanation:

Line FG contains points F( 3,7 ) and G( -4,-5 )

and HI contains points H( -1,0 ) and I ( 4, 6 )

Now we have to find these lines are parallel or perpendicular.

If these lines are parallel then slope FG and HI line will same.

Similarly if lines are perpendicular then multiplications of the slopes of these lines will be = -1

Slope of FG
`(m_(1)) = (y-y')/(x-x') =((7+5)/(3+4))=(12)/(7)`

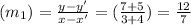
Now slope of HI
`(m_(2)) =(6-0)/(4+1)=(6)/(5)`

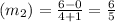
For parallel lines
`m_(1)` should be equal to
`m_(2)`

But
`(12)/(7)` ≠
`(6)/(5)` so lines are not parallel.

For perpendicular lines
`m_(1)` ×
`m_(2)` = -1

But
`(12)/(7)` ×
`(6)/(5)` =
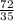`(72)/(35)` ≠ -1

So lines are neither parallel nor perpendicular.

Option C neither is the answer.