Question

Find the 12th partial sum of 
∞
∑  (-2i-10)
i-1

Answer 1

Hello,



`$\sum_(i=1)^(12)(-2i-10)=-10\sum_(i=1)^(12)1-2\sum_(i=1)^(12)i$`


`=-120-2*13*12/2=-120-156=-276`

Answer 2

The 12th partial sum of the given series is:

-276

Explanation:

We are asked to find the 12th partial sum of the series which is given by:

`\sum_(i=1)^(\infty)(-2i-10)`

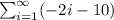
i.e. we have to find the sum of first 12 terms.

i.e.

`\sum_(i=1)^(12)(-2i-10)`

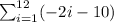
which could also be simplified by the method:

`\sum_(i=1)^(12)(-2i-10)=-2\sum_(i=1)^(12)i-10\sum_(i=1)^(12)1`

which is further given by:

`\sum_(i=1)^(12)(-2i-10)=-2* (1+2+3+4+5+6+7+8+9+10+11+12)-10* (1+1+1+1+1+1+1+1+1+1+1+1)`

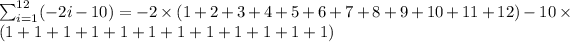
know we know that:

`1+2+3+.....+n=(n(n+1))/(2)`

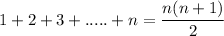
i.e.

`1+2+3+....+12=(12* 13)/(2)\\\\1+2+3+....+12=78`

Hence, we get:

`\sum_(i=1)^(12)(-2i-10)=-2* 78-10* 12\\\\[tex]\sum_(i=1)^(12)(-2i-10)=-156-120\\\\[tex]\sum_(i=1)^(12)(-2i-10)=-276`

Hence, the answer is: -276