Question

Aya = a1 + (n - 1)d

Find the 26th term of an arithmetic sequence with ai = -33 and d= 4.
O 67
O-130
O 71
O-129

Answer 1

The 26th term of an arithmetic sequence is:

`a_(26)=67`

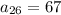
Hence, option A is true.

Explanation:

Given

• a₁ = -33

• d = 4

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

substituting a₁ = -33 and d = 4 in the nth term of the sequence

`a_n=-33+\left(n-1\right)4`

`\:a_n=-33+4n-4`

`a_n=4n-37`

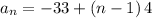
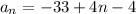
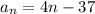
Thus, the nth term of the sequence is:

`a_n=4n-37`

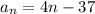
now substituting n = 26 in the nth term to determine the 26th term of the sequence

`a_n=4n-37`

`a_(26)=4\left(26\right)-37`

`a_(26)=104-37`

`a_(26)=67`

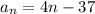
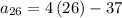
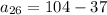
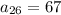
Therefore, the 26th term of an arithmetic sequence is:

`a_(26)=67`

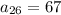
Hence, option A is true.