Answer:
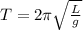
Explanation:
The period of oscilations in a pendulum is defined as
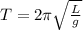
Where
 is the length of the string and
is the length of the string and
 is gravity.
is gravity.
Notice that the pendulum is oscillating due to gravity in the first place. Then, that acceleration of gravity is affected by the acceleartion of the elevator, which is
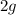 . We know that acceleration is a vector, which means the net acceleration would be
. We know that acceleration is a vector, which means the net acceleration would be
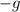 of gravity and
of gravity and
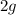 of the elevator, which gives us
of the elevator, which gives us
 .
.
Having said that, the perior of oscaillations would be the same
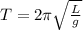
Because, the net acceleartion is also the same but in different direction.