Question

A new airport is in its planning phase. One particular challenge is that there are several tall buildings in the vicinity. In particular, there's a 450-foot-tall building that is 2500 feet (ground distance) directly East from the end of the runway. The steepest angle the airplane can climb upon takeoff is 15°. Given this scenario, could an airplane take off and clear this tall building?

Answer 1

Could an airplane take off and clear this tall building? YES

Explanation:

Trigonometry

The building and the ground form a right (90°) angle. The path of the airplane (assumed a straight line) completes the right triangle.

The takeoff angle of the plane θ=15° has the height of the building (450 feet) as the opposite side and the horizontal distance from the end of the runway (2500 feet) as the adjacent side.

The tangent of θ is defined as the following ratio:

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

`\displaystyle \tan \theta=(450)/(2500)`

`\displaystyle \tan \theta=0.18`

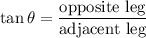
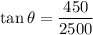
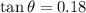
Calculating the inverse tangent function:

`\theta=\arctan 0.18`

`\theta\approx 10^\circ`

This means the angle needed to clear the tall building is about 10° and it's within the maximum airplane's takeoff angle.

Could an airplane take off and clear this tall building? YES