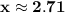Question

MHANIFA HELP ME 10 POINTS
3^x= 3*2^x
solve this equation

Answer 1

`\displaystyle x=(\log 3)/(\log(3)-\log 2)\approx 2.71`

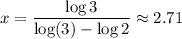
Explanation:

Logarithms

We need to recall these properties of logarithms:

`\log_ax^n=m\log_ax`

`\log_a(xy)=\log_a(y)+\log_a(y)`

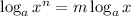
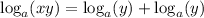
The equation to solve is:

`3^x=3*2^x`

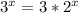
Applying logarithms:

`\log(3^x)=\log(3*2^x)`

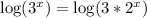
Applying the exponent property on the left side and the product property on the right side:

`x\log(3)=\log 3+\log 2^x`

Applying the exponent property:

`x\log(3)=\log 3+x\log 2`

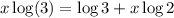
Rearranging:

`x\log(3)-x\log 2=\log 3`

Factoring:

`x(\log(3)-\log 2)=\log 3`

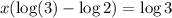
Solving:

`\boxed{\displaystyle x=(\log 3)/(\log(3)-\log 2)}`

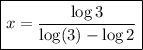
Calculating:

`\mathbf{x\approx 2.71}`