Question

Compare the perimeters of the two regular figures. Which statement is true?

A. The perimeter of the octagon is greater than that of the hexagon.
B. The perimeter of the hexagon is greater than that of the octagon.
C. The perimeters are equivalent.
D. It is impossible to determine which perimeter is greater.

Answer 1

(A). The perimeter of the octagon is greater than that of the hexagon.

Explanation:

Since, hexagon consists of 6 sides and 6 angles, thus the measure of one angle of the hexagon will be=
`\frac{(n-2){\timeS}180^(\circ)}{6}`

=
`\frac{(6-2){\timeS}180^(\circ)}{6}`

=
`\frac{(4){\timeS}180^(\circ)}{6}`

=
`120^(\circ)`

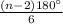
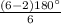
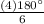
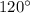
Now, since MQ is the angle bisector of the one of the angle of the hexagon, therefore ∠QMP=60°.

Now, from ΔQMP. we have

`(MP)/(MQ)=cos60^(\circ)`

`MP=(1)/(2)`

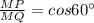
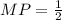
Thus, the perimeter of the hexagon is:

`P=12{*}MP`

`P=12{*}(1)/(2)`

`P=6 units`

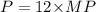
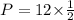
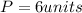
Thus, the perimeter of hexagon is 6 units.

Also, Since, octagon consists of 8 sides and 8 angles, thus the measure of one angle of the octagon will be=
`\frac{(n-2){\timeS}180^(\circ)}{8}`

=
`\frac{(8-2){\timeS}180^(\circ)}{8}`

=
`\frac{(6){\timeS}180^(\circ)}{8}`

=
`135^(\circ)`

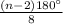
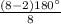
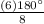
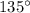
Now, since AP is the angle bisector of the one of the angle of the octagon, therefore
`{\angle}PAC=cos(135)/(2)`.

From ΔAPC, we have

`AC=cos(135)/(2)`

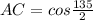
Now, Perimeter of octagon is:

`P=16{*}cos(135)/(2)`

`P=16{*}0.382`

`P=6.122 units`

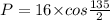
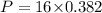
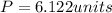
Thus, the perimeter of octagon is 6.122 units.

Now, the perimeter of octagon is greater than perimeter of the hexagon, thus option A is correct that is The perimeter of the octagon is greater than that of the hexagon.