Question

write x2 − 8x 13 = 0 in the form (x − a)2 = b, where a and b are integers. (x − 4)2 = 3 (x − 3)2 = 2 (x − 2)2 = 1 (x − 1)2 = 4

Answer 1

Option 1st is correct

`(x-4)^2 = 3`

Explanation:

Given equation:

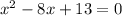`x^2-8x+13=0` .....[1]

To write the given equation in the form of
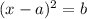`(x-a)^2 = b` where, a and b are integers

Subtract 13 from both sides in [1] we have;

`x^2-8x=-13`

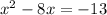
Complete the square in x-term by adding the square of half the x-coefficient
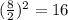`((8)/(2))^2 = 16` we have;

`x^2-8x+4^2 = -13+16`

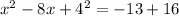
Using identity rules:
`(a-b)^2 = a^2-2ab+b^2`

then;

`(x-4)^2 = 3`

Therefore, the the given equation in the form of
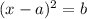`(x-a)^2 = b` is ,
`(x-4)^2 = 3`

Answer 2

x^2 -8x + 13 =0

x^2 -8x = -13

x^2 - 8x +16 = - 13 + 16

(x - 4)^ = 3 That is the first option shown.