Question

Three dogs (Spot, Fido, and Steinberg) are pulling on a chew toy. The chew toy is experiencing no acceleration. Spot is pulling with a force of 30 Newtons directly South. Fido is pulling with a force of 20 Newtons at an angle of 63 degrees North of East. What are the magnitude and direction of the force that Steinberg is applying?

Answer 1

The magnitude and direction of the force applied by Steinberg are approximately 15.192 newtons and 126.704º.

Step-by-step explanation:

The chew toy is at equilibrium and experimenting three forces from three distinct dogs. The Free Body Diagram depicting the system is attached below. By Newton's Laws we construct the following equations of equilibrium: (Sp is for Spot, F is for Fido and St is for Steinberg) All forces and angles are measured in newtons and sexagesimal degrees, respectively:

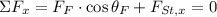`\Sigma F_(x) = F_(F)\cdot \cos \theta_(F) + F_(St,x) = 0` (1)

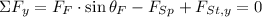`\Sigma F_(y) = F_(F)\cdot \sin \theta_(F)-F_(Sp)+F_(St,y) = 0` (2)

If we know that
`F_(F) = 20\,N`,
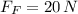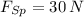`F_(Sp) = 30\,N` and
`\theta_(F) = 63^(\circ)`, then the components of the force done by Steinberg on the chewing toy is:

`F_(St,x) = -F_(F)\cdot \cos \theta_(F)`

`F_(St,x) = -(20\,N)\cdot \cos 63^(\circ)`

`F_(St, x) = -9.080\,N`

`F_(St,y) = F_(Sp)-F_(F)\cdot \sin \theta_(F)`

`F_(St,y) = 30\,N-(20\,N)\cdot \sin 63^(\circ)`

`F_(St, y) = 12.180\,N`

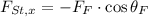
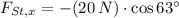
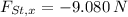
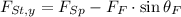
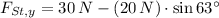
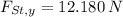
The magnitud of the force is determined by Pythagorean Theorem:

`F_(St) = \sqrt{F_(St,x)^(2)+F_(St,y)^(2)}`

`F_(St) =\sqrt{(-9.080\,N)^(2)+(12.180\,N)^(2)}`

`F_(St) \approx 15.192\,N`

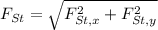
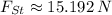
Since the direction of this force is in the 3rd Quadrant on Cartesian plane, we determine the direction of the force with respect to the eastern semiaxis:

`\theta_(St) = 180^(\circ) + \tan^(-1) \left((F_(St,y))/(F_(St,x))\right)`

`\theta_(St) = 180^(\circ) + \tan^(-1) \left((12.180\,N)/(-9.080\,N)\right)`

`\theta_(St) \approx 126.704^(\circ)`

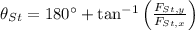
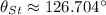
The magnitude and direction of the force applied by Steinberg are approximately 15.192 newtons and 126.704º.