Question

A polynomial function can be written as (x − 1)(x − 4)(x + 7). What are the x-intercepts of the graph of this function?

a (1, 0), (4, 0), (7, 0)
b (−1, 0), (−4, 0), (−7, 0)
c(1, 0), (4, 0), (−7, 0)
d (−1, 0), (−4, 0), (7, 0)

Answer 1

(x - 1)(x - 4)(x + 7) = 0 ⇔ x - 1 = 0 or x - 4 = 0 or x + 7 = 0

x = 1 or x = 4 or x = -7

Answer: c. (1; 0); (4; 0); (-7; 0)

Answer 2

Option c is correct

(1, 0), (4, 0) and (-7, 0)

Explanation:

x-intercepts states that the line cut the x-axis.

Substitute y = 0 and solve for x.

As per the statement:

A polynomial function can be written as (x − 1)(x − 4)(x + 7).

⇒y = (x − 1)(x − 4)(x + 7)

By definition of x-intercept:

Substitute y =0 we have;

`(x-1)(x-4)(x+7)=0`

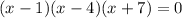
By zero product property we have;

x-1 =0 , x-4 = 0 and x+7 =0

⇒x = 1, x = 4 and x = -7

⇒x-intercepts = (1, 0), (4, 0) and (-7, 0)

therefore, the x-intercepts of the graph of this function is, (1, 0), (4, 0) and (-7, 0)