Question

Solve each system graphically. Be sure to check your solution. If a system has an infinite number of solution, use set-builder notation to write the solution set .If a system has no solution, state this. x=y-4 2x=4y

Answer 1

To solve a system of equations graphically, we need to graph the equations. We need two points to graph a line. Substituting y = 0 into the equation of the first line, we get:

`\begin{gathered} x=y-4 \\ x=0-4 \\ x=-4 \end{gathered}`

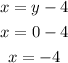
Then, the line passes through the point (-4, 0). Substituting y = 4 into the equation of the first line, we get:

`\begin{gathered} x=4-4 \\ x=0 \end{gathered}`

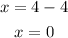
Then, the line passes through the point (0, 4).

Now, considering the second line, substituting with y = 0 and y = 1, and solving for x, we get:

`\begin{gathered} 2x=4y \\ 2x=4\cdot0 \\ 2x=0 \\ x=(0)/(2) \\ x=0 \end{gathered}`
`\begin{gathered} 2x=4\cdot1 \\ x=(4)/(2) \\ x=2 \end{gathered}`

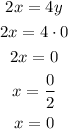
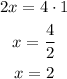
Therefore, this line passes through the points (0, 0) and (2,1).

Connecting these points, each line is graphed as follows:

The solution to the system of equations is the point at which both lines intersect. From the graph, the solution is (-8, -4)