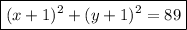Question

Find an equation of the circle that satisfies the stated conditions.(give your answer in standard notation.)

Endpoints of diameter A(4,-9)and B(-6,7)

Answer 1

`(x+1)^2+(y+1)^2=89`

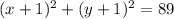
Explanation:

Equation of a Circle

A circle centered in the point (h,k) and with radius r, can be expressed with the equation:

`(x-h)^2+(y-k)^2=r^2`

We are given the endpoints of the diameter of a circle as A(4,-9) and B(-6,7).

The center of the circle is the midpoint of segment AB. The midpoint (xm,ym) has coordinates:

`\displaystyle x_m=(4-6)/(2)=(-2)/(2)=-1`

`\displaystyle y_m=(-9+7)/(2)=(-2)/(2)=-1`

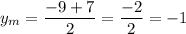
Center of the circle: (-1,-1)

The radius is half the diameter and the diameter is the distance between the endpoints.

Given two points A(x1,y1) and B(x2,y2), the distance between them is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

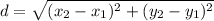
The diameter is:

`d=√((-6-4)^2+(7+9)^2)=√(100+256)=√(356)=2√(89)`

The radius is:

`r=2√(89)/2=√(89)`

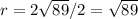
The equation of the circle is:

`(x+1)^2+(y+1)^2=√(89)^2`

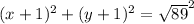
Squaring the root:

`\boxed{(x+1)^2+(y+1)^2=89}`