Question

1. Priya is buying raisins and almonds to make trail mix. Almonds cost $5.20 perpound and raisins cost $2.75 per pound. Priya spent $11.70 buying almondsand raisins. The relationship between pounds of almonds a, pounds of raisinsr,and the total cost is represented by the equation 5.20a - 2.75r = 11.70.

Answer 1

The variables are:

• a: pounds of almonds

,

• r: pounds of raisins

The total cost is represented by the equation:

`5.20a+2.75r=11.70`

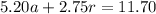
a. Substituting into the above equation with a = 2, and solving for r:

`\begin{gathered} 5.20\cdot2+2.75r=11.70 \\ 10.40+2.75r=11.70 \\ 10.40+2.75r-10.40=11.70-10.40 \\ 2.75r=1.30 \\ (2.75r)/(2.75)=(1.30)/(2.75) \\ r\approx0.47 \end{gathered}`

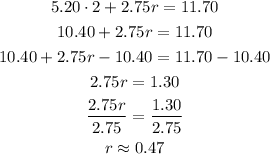
Priya bought approximately 0.47 pounds of raisins

b. Substituting into the above equation with a = 1.06, and solving for r:

`\begin{gathered} 5.20\cdot1.06+2.75r=11.70 \\ 5.512+2.75r=11.70 \\ 5.512+2.75r-5.512=11.70-5.512 \\ 2.75r=6.188 \\ (2.75r)/(2.75)=(6.188)/(2.75) \\ r\approx2.25 \end{gathered}`

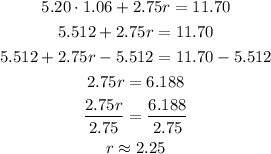
Priya bought approximately 2.25 pounds of raisins

c. Substituting into the above equation with a = 0.64, and solving for r:

`\begin{gathered} 5.20\cdot0.64+2.75r=11.70 \\ 3.328+2.75r=11.70 \\ 3.328+2.75r-3.328=11.70-3.328 \\ 2.75r=8.372 \\ (2.75r)/(2.75)=(8.372)/(2.75) \\ r\approx3.04 \end{gathered}`

Priya bought approximately 3.04 pounds of raisins

d. Isolating r from the equation, we get:

`\begin{gathered} 5.20a+2.75r=11.70 \\ 5.20a+2.75r-5.20a=11.70-5.20a \\ 2.75r=11.70-5.20a \\ (2.75r)/(2.75)=(11.70-5.20a)/(2.75) \\ r=(11.70)/(2.75)-(5.20a)/(2.75) \\ \text{ Simplifying} \\ r=(234)/(55)-(104)/(55)a \end{gathered}`