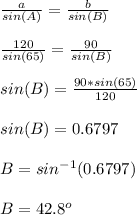Question

A surveyer wants to find the distance from points A and B and to an inaccessible point C. These three points form a triangle. Because points he can be cited from both A and B, he knows that the measure of angle a equals 65°. Also, it is known that the distance from A-to-C is 90 m and the distance from B to C is 120 m. What is the measure of angle B

Answer 1

42.8°

Explanation:

The sine rule states that for a triangle with lengths of a, b and c and the corresponding angles which are opposite the sides as A, B and C, then the following rule holds:

`(a)/(sin(A))=(b)/(sin(B)) =(c)/(sin(C))`

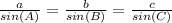
Given that points A, B and C forms a triangle with angle A = 65°, distance from A-to-C = 90 m and the distance from B to C = 120 m.

The distance from A to C is the side opposite to angle B. Hence let b = distance from A to C = 90 m.

The distance from B to C is the side opposite to angle A. Hence let a = distance from B to C = 120 m.

Therefore using sine rule:

`(a)/(sin(A))=(b)/(sin(B)) \\\\(120)/(sin(65))=(90)/(sin(B)) \\\\sin(B)=(90*sin(65))/(120) \\\\sin(B) =0.6797\\\\B=sin^(-1)(0.6797)\\\\B=42.8^o`