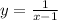Question

Give an example of a rational function that has no horizontal asymptote and a vertical asymptote at

x = 1.

Answer 1

For this case, the first thing we are going to do is define variables.

We have then:

x: independent variable

y: dependent variable

We write the rational function with vertical asintotal.

We have then:

`image`

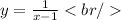
Since the denominator must be nonzero, then we have:

`image`

Therefore, we have a vertical asymptote at x = 1

Answer:

an example of a rational function that has no horizontal asymptote and a vertical asymptote at x = 1 is:

`y =(1)/(x-1)`

Answer 2

This means that we will have the domain:
x ∈ R \ { 1 }
An example: f ( x ) = x³ / x - 1 ( no horizontal asymptote and vertical asymptote at x = 1 )