Answer:
(a) Θ =
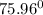
(b)
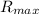 is achieved when T =
is achieved when T =
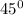 , thus
, thus
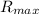 = R ÷ Sin2T
= R ÷ Sin2T
(c) Yes
Step-by-step explanation:
(a) Max. height (
 ) =
) =
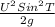
Range (R) =
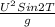
where T represents theta
So for, R =

⇒
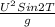 =
=
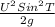
Using trigonometric functions,
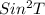 = 2SinTCosT =
= 2SinTCosT =

⇒ 4 = Tan T
T =
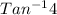
=
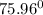
∴ Theta =
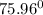
(b) Since, R =
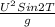
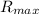 is achieved when T =
is achieved when T =
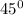
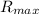 =
=
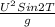
∴
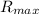 = R ÷ Sin2T
= R ÷ Sin2T