Question

Solve for x: |x − 2| + 10 = 12

x = 0 and x = 4
x = −4 and x = 0
x = −20 and x = 4
No Solution

Answer 1

Option A is correct.

Values of x :

x = 0 and x =4

Explanation:

Absolute function states that contains an algebraic expression within absolute value symbols i,e

`|x| = \left\{\begin{matrix}x & if x>0 \\ 0 & if x = 0\\ -x & if x< 0 \end{matrix}\right.`

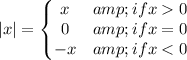
Given that:
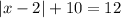`|x-2|+10=12` .....[1]

solve for x;

Subtract 10 from both sides in equation [1] we get;

`|x-2|+10-10=12-10`

Simplify:

`|x-2|=2`

By definition of Absolute;

(x-2) = 2 and -(x-2) = 2

or

x-2 =2 and x -2 = -2

we have;

x = 2+2 and x= -2+2

x = 4 and x = 0

Therefore, the value of x are 4 and 0.

Answer 2

|x − 2| + 10 = 12

|x − 2| =2
x-2=+-2
x-2=2 and x-2=-2
x=4 and x=0