The number -8.3 belongs to the rational numbers, as it can be expressed in fractional form.
All the rational numbers are real numbers.
-8.3 is not a whole or integer number.
The answer is A (rational), as it is the most specific.
2) Dilation of a rectangle
We have to dilate it by a factor of 2/3.
Each coordinate will be multiplied by 2/3.
We need to calculate the perimeter of the new rectangle.
The rectangle has sides of length 4 and 8.
If they are dilated by 2/3, we would get a new rectangle with sides 2/3*4=8/3 and 2/3*8=16/3.
The perimeter can be calculated multipling the sum of the sides by 2:
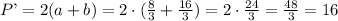
The perimeter of the new rectangle is 16.
We could have arrived to the same solution if we multiply the perimeter of the original rectangle by the scale factor.
The perimeter of the original rectangle is 2(4+8)=2*12=24.
If we multiply it by 2/3 we get 24*2/3=48/3=16.