Answer:
Explanation:
Given is an implicit function of y in x.
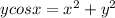
The steps shown were the differentiation on both the sides
Left side done using product rule as well as chain rule and right side addition rule and chain rule
The steps got as
 is correct
is correct
Next step is to group all dy/dx terms together
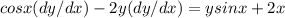 is also right step
is also right step
Now rewrite left side as

Thus both the steps and answer are correct.