Question

1. Identify the vertical asymptotes of f(x) = 2/x^2+3x-10

2. Identify the vertical asymptotes of f(x) = x+6/x^2-9x +18
3. Identify the horizontal asymptote of f(x) =4x/7
4. Identify the horizontal asymptote of f(x) = 7x+1/2x-9
5. Identify the horizontal asymptote of f(x) = x^2+5x-3/4x-1
6. Identify the oblique asymptote of f(x) = x^2-4x+8 /x+2
7.Identify the oblique asymptote of f(x) = 2x^2+3x+8/x+3
8.Identify the oblique asymptote of f(x) = x+4/3x^2+5x-2
9. Identify the oblique asymptote of f(x) =4x^2-x+2/x+1

Answer 1

1)Vertical asymptote is x=0
2)f(x) = 2/(x² + 3x - 10) = 2 / [(x + 5)(x - 2)]
Vertical asymptotes are x=2 and x=-5.
3)It's a linear function, just a line, with a slope of 4/7 and a y-intercept of 0 because b=0.the degree of the numerator is 1 and the degree of the denominator is 0. 1>0 so we do not have any horizontal asymptotes.
4) y = (7x+1)/(2x-9)
2xy - 9y = 7x + 1
2xy - 7x = 9y+1
x = (9y + 1) / (2y - 7)
y=7/2
5)
6), y=x−6 is your oblique asymptote
7) line y=2x−3
8)There is a horizontal asymptote and two vertical asymptotes though.
They are y=0,x=13,andx=−2
9)The oblique or slant asymptote is 4x−5.

Answer 2

1.Vertical asymptotes are at x=-5 and x=2 .

2.Vertical asymptotes are at x=6 and x=3.

3.No , horizontal asymptotes.

4.Horizontal asymptote
`y=(7)/(2)`.

5.No, horizontal asymptote.

6.Oblique asymptote at
`y= x-6`.

7.Oblique asymptote at y=2x-3

8.There is no oblique asymptote.

9.Oblique asymptote y=4x-5.

Explanation:

1. To find vertical asymptote

Substitute denominator is equal to zero

Therefore,
`x^2+3x-10=0`

Factorize the polynomial we get

`(x+5)(x-2)=0`

`x+5=0` and
`x-2=0`

`x=-5` and
`x=2`

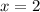
Hence, the vertical asymptote of f(x) at x= -5 and x=2

2.
`x^2-9x+18=0`

Fatorize the polynomial then we get

`(x-6)(x-3)=0`

`x-6=0` and
`x-3=0`

`x=6` and
`x=3`.

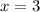Therefore, the vertical asymptote of f(x) at x=6 and x=3

3.There is no horizontal asymptote of f(x) because the degree of numerator is greater than the degree of denominator.

4.Horizontal asymptote : The degree of numerator and degree of denominator are same therefore,

Horizontal asymptote=
`(7)/(2)`.

5.No horizontal asymptote because the degree of numerator is greater than the degree of denominator.

6.Oblique asymptote: oblique asymptote is the value of quotient which obtained by dividing the numerator by denominator .

Oblique asymptote of f(x) at y=x-6

7. Oblique asymptote of f(x) at y= 2x-3

8. There is no oblique asymptote because the degree of numerator is less than the degree of denominator.

9.Oblique asymptote of f(x) at y= 4x-5