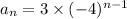Question

Find an explicit rule for the nth term of a geometric sequence where the second and fifth terms are -12 and 768, respectively

Answer 1

`a_2=-12;\ a_5=768\\\\a_n=a_1r^(n-1)\\\\a_5:a_2=r^3\\\\r^3=768:(-12)\\\\r^3=-64\\\\r=\sqrt[3]{-64}\\\\r=-4\\\\a_1=a_2:r\to a_1=-12:(-4)=3\\\\\boxed{a_n=3\cdot(-4)^(n-1)}`

Answer 2

Nth term is given by
`a_n=3* (-4)^(n-1)`

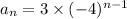
Explanation:

For a geometric progression we have expression for nth term

`a_n=ar^(n-1)`

where a is first term and r is common ratio.

Here the second and fifth terms are -12 and 768.

That is

a₂ = ar²⁻¹ = ar = -12

a₅ = ar⁵⁻¹ = ar⁴ = 768

Dividing we will get

`(ar^4)/(ar)=(768)/(-12)\\\\r^3=-64\\r=-4`

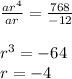
Substituting in

ar = -12

a x -4 = -12

a = 3

Nth term is given by
`a_n=3* (-4)^(n-1)`