Question

At 1.00 atm and 0 °C, a 5.04 L mixture of methane (CH4) and propane (C3H8) was burned, producing 16.5 g of CO2. What was the mole fraction of each gas in the mixture? Assume complete combustion.

Answer 1

The mole fraction of methane in the mixture of methane and propane is 0.667, while the mole fraction of propane is 0.333.

Step-by-step explanation:

To find the mole fraction of each gas in the mixture, we need to first calculate the moles of methane and propane in the mixture.

From the balanced equation for the complete combustion of propane (C3H8): C3H8 + 5O2 → 3CO2 + 4H2O, we can see that for every mole of propane, we produce 3 moles of CO2.

Given that 16.5 g of CO2 was produced, we can calculate the moles of CO2: 16.5 g CO2 * (1 mol CO2/44.01 g CO2) = 0.375 mol CO2.

Since 1 mole of propane produces 3 moles of CO2, we can calculate the moles of propane: 0.375 mol CO2 * (1 mol propane/3 mol CO2) = 0.125 mol propane.

The moles of methane can be calculated by subtracting the moles of propane from the total number of moles in the mixture: Moles of methane = Total moles - Moles of propane = 0.375 mol - 0.125 mol = 0.25 mol.

To find the mole fractions, divide the moles of each gas by the total moles in the mixture:

Mole fraction of methane = Moles of methane / Total moles = 0.25 mol / 0.375 mol = 0.667

Mole fraction of propane = Moles of propane / Total moles = 0.125 mol / 0.375 mol = 0.333

Answer 2

Answer: The mole fraction of methane is 0.67 and that of propane is 0.33

Step-by-step explanation:

• The equation given by ideal gas follows:

`PV=nRT`

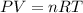
where,

P = pressure of the mixture = 1.00 atm

V = Volume of the mixture = 5.04 L

T = Temperature of the mixture =
`0^oC=[0+273]K=273K`

R = Gas constant =
`0.0821\text{ L. atm }mol^(-1)K^(-1)`

n = number of moles of mixture = ?

Putting values in above equation, we get:

`1.00atm* 5.04L=n_(mix)* 0.0821\text{ L atm }mol^(-1)K^(-1)* 273K\\n_(mix)=(1.00* 5.04)/(0.0821* 273)=0.225mol`

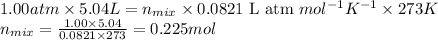
Let the number of moles of methane be 'x' moles and that of propane be 'y' moles

So,
`x+y=0.225` .....(1)

• The chemical equation for the combustion of methane follows:

`CH_4+2O_2\rightarrow CO_2+2H_2O`

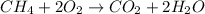
By Stoichiometry of the reaction:

1 mole of methane produces 1 mole of carbon dioxide

So, 'x' moles of methane will produce =
`(1)/(1)* x=x` moles of carbon dioxide

• The chemical equation for the combustion of propane follows:

`C_3H_8+5O_2\rightarrow 3CO_2+4H_2O`

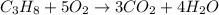
By Stoichiometry of the reaction:

1 mole of propane produces 3 mole of carbon dioxide

So, 'y' moles of propane will produce =
`(1)/(1)* y=y` moles of carbon dioxide

• Evaluating mass of carbon dioxide:

Total moles of carbon dioxide = (x + 3y)

Mass of carbon dioxide = (Total moles) × (Molar mass of carbon dioxide)

Molar mass of carbon dioxide = 44 g/mol

Mass of carbon dioxide =
`(x+3y)* 44`

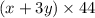
We are given:

Mass of carbon dioxide = 16.5 g

So,
`44(x+3y)=16.5` .....(2)

Putting value of 'x' from equation 1, in equation 2, we get:

`44(0.225-y+3y)=16.5\\\\0.225+2y=0.375\\\\y=(0.15)/(2)=0.075`

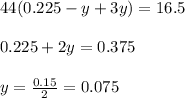
Evaluating value of 'x' from equation 1, we get:

`x+0.075=0.225\\x=0.15`

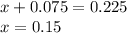
• Mole fraction of a substance is given by:

`\chi_A=(n_A)/(n_A+n_B)`

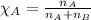
For Methane:

Moles of methane = 0.15 moles

Total moles = 0.225

Putting values in above equation, we get:

`\chi_((Methane))=(0.15)/(0.225)=0.67`

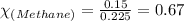
For Propane:

Moles of propane = 0.075 moles

Total moles = 0.225

Putting values in above equation, we get:

`\chi_((Propane))=(0.075)/(0.225)=0.33`

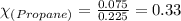
Hence, mole fraction of methane is 0.67 and that of propane is 0.33