2/9
Step-by-step explanation
The probability of an event is the number of favorable outcomes divided by the total number of outcomes possible
Step 1
Let
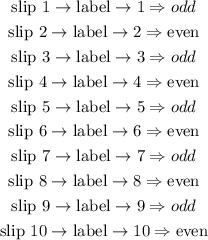
hence:
total of even numbers: 5
total odd numbers: 5
total outcomes= 10
Step 2
a)
now, the probability of selecting an odd number
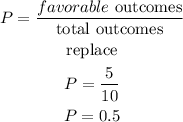
b) now, if the slip is not replaced we would have
total of even numbers: 5
total odd numbers: 4
total outcomes= 9
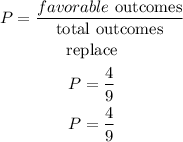
finally, the probality of both events happen is the product of the individual probabilities
so
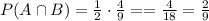
therefore, the answer is 2/9
I hope this helps you