Question

If the function f(x) = mx + b has an inverse function, which statement must be true?

m=/0

m = 0

b=/0

b = 0

Answer 1

The inverse function of the function f(x) = mx + b can be determined by expressing the function in terms of x alone. hence, (y - b)/m = x. Then we exhange x and y, to result to (x - b)/m = y. In this case, m is not equal to zero. The answer to this problem hence is A>

Answer 2

we have

`f(x)=mx+b`

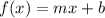
Find the inverse of f(x)

Let

`y=f(x)`

`y=mx+b`

Exchanges the variables x for y and y for x

`x=my+b`

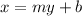
isolate the variable y

`my=x-b`

`y=(x-b)/(m)`

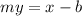
Let

`f(x)^(-1) =y`

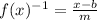`f(x)^(-1)=(x-b)/(m)` -----> inverse function

Hence

In the inverse function the denominator can not be zero, therefore the value of m can not be equal zero

the answer is the option

`m\\eq 0`