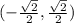Answer:
Part 1:
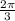 radians
radians
Part 2: The minute hand travels
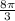 inches.
inches.
Part 3: The minute hand travels
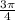 radians.
radians.
Part 4: The coordinate point is
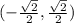
Explanation:
Part 1:
There are 60 minutes in an hour. 1 hour is 1 revolution (1 circle), which is 360°.
So each minute represents
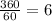 degrees
degrees
From 3:35 to 3:55 is 20 minutes. Hence, 20 minutes is
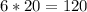 degrees.
degrees.
To convert from degrees to radians, we multiply the degrees by

120° is equal to
 radians
radians
Part 2:
We want to find the "arc length" of this.
Formula for arc length is
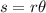
Where,
- s is the arc length
- r is the radius (here the minute hand was given as 4 inches)
 is the angle in radians (we found it to be
is the angle in radians (we found it to be
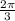 )
)
So,
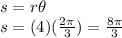
The minute hand travels
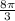 inches.
inches.
Part 3:
Here we use the arc length formula where we want to find
 given that
given that
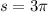 and radius is 4 inches. So we have:
and radius is 4 inches. So we have:

The minute hand travels
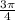 radians.
radians.
Part 4:
The coordinate point associated with a specif radian is given by the formula:
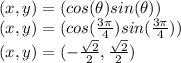
Thus the coordinate point is