Question

Find the equation of a line parallel to the line 2x-y-9=0 and passing through the point of intersection of the lines 5x+y+4=0 and 2x+3y=1

Answer 1

`y=2x-3`

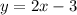
Explanation:

1. Using the point of intersections, we use the substitution method to find the coordinates of the line parallel to
`2x-y-9=0`

`5x+y+4=0`

`y= -4-5x`

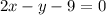
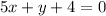
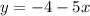
substituting the value of y in
`2x+3y=1`:

`2x +3(-4-5x)=1\\\\2x-12-15x-1=0\\-13x=13x\\x= (13)/(-13)= -1`

substituting x=-1 in y= -4-5x:

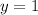`y= 1` (upon solving, you should get this)

`(x,y)= (-1,1)`

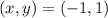
2. Using y=mx+c and making y the subject of the formula 2x-y-9=0 and using the coordinate we found earlier, we will find the equation of the parallel line. (We make y the subject of the formula to find the gradient)

`2x-y-9=0\\2x-9=y\\y= 2x-9`

`y= mx+c\\`

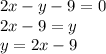
-1= 2 x 1 +c

-3=c

• y= 2x-3