Answer:
y-axis only.
Explanation:
The given equation is
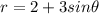
Notice that this equation is in polar form.
If
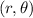 can be replace with
can be replace with
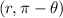 or
or
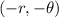 , then the graph is symmetric to the line
, then the graph is symmetric to the line
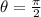 , which is a vertical line.
, which is a vertical line.
Let's evaluate the given equation.
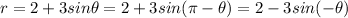
But,
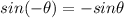
So,
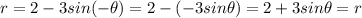
Notice that the change produces the same equation.
Therefore, the given polar expression is symmetric to
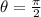 , which is the y-axis only in the coordinate system.
, which is the y-axis only in the coordinate system.
So, the right answer is y-axis only.