Question

What is the local minimum value of the function? (Round answer to the nearest hundredth) g(x)=x^4-5x^2+4

Answer 1

The local minimum of function is an argument x for which the first derivative of function g(x) is equal to zero, so:
g'(x)=0
g'(x)=(x^4-5x^2+4)'=4x^3-10x=0
x(4x^2-10)=0
x=0 or 4x^2-10=0
4x^2-10=0 /4
x^2-10/4=0
x^2-5/2=0
[x-sqrt(5/2)][x+sqrt(5/2)]=0

Now we have to check wchich argument gives the minimum value from x=0, x=sqrt(5/2) and x=-sqrt(5/2).
g(0)=4
g(sqrt(5/2))=25/4-5*5/2+4=4-25/4=-9/4
g(-sqrt(5/2))=-9/4
The answer is sqrt(5/2) and -sqrt(5/2).

Answer 2

-1.58 and 1.58

Explanation:

We can determine the local minimum value using the derivative test. We can take the derivative of the function g(x):

g'(x)= (d/dx)g(x)

g'(x)

`=4\cdot(x^3)-10\cdot(x)`

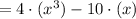
We find the x values at which the function is zero:

`2\cdot(x)\cdot(2\cdot(x^2)-5)=0`

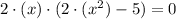
Therefore x=0, x=±√5/2

To find the minimum value we substitue our values x=0 or x=-√5/2 or x=√5/2 into g(x)

g(0)=4

g(-√5/2)=-9

g(√5/2)=-9

Therefore the local minimum is -1.58 and 1.58.