Question

Match the range of the function f(x) = x2 + 2x − 1 to its domain.

2 -2 3 -3

2 -->

14 -->

7 -->

-1 -->

Answer 1

(2,7) , (-2,-1) , (3,14) , (-3,2)

Explanation:

Given : Function
`f(x)=x^2+2x-1`

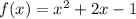
To find : Match the range of the function to its domain ?

Solution :

Domain is x and range is y,

We substitute the domain values 2, -2, 3, -3 and find y,

At x=2

`f(2)=(2)^2+2(2)-1`

`f(2)=4+4-1`

`f(2)=7`

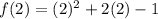
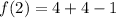
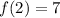
i.e. (2,7)

At x=-2

`f(-2)=(-2)^2+2(-2)-1`

`f(-2)=4-4-1`

`f(-2)=-1`

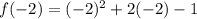
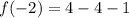
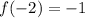
i.e. (-2,-1)

At x=3

`f(3)=(3)^2+2(3)-1`

`f(3)=9+6-1`

`f(3)=14`

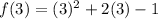
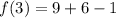
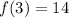
i.e. (3,14)

At x=-3

`f(-3)=(-3)^2+2(-3)-1`

`f(-3)=9-6-1`

`f(-3)=2`

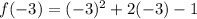
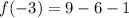
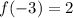
i.e. (-3,2)

Answer 2

f(x) = x² + 2x - 1

f(2) = 2² + 2 · 2 - 1 = 4 + 4 - 1 = 7
f(-2) = (-2)² + 2 · (-2) - 1 = 4 - 4 - 1 = -1
f(3) = 3² + 2 · 3 - 1 = 9 + 6 - 1 = 14
f(-3) = (-3)² + 2 · (-3) - 1 = 9 - 6 - 1 = 2

The range = {-1; 2; 7; 14}