Answer:
f --> d
f' --> c
f'' --> b
f''' --> a
Explanation:
The derivative of a function
 is another function
is another function
 which values are the slope of the line tangent to the curve
which values are the slope of the line tangent to the curve
 at the point
at the point
 .
.
So the derivative at some point will be:
- Positive if the line tangent at the curve at that point has a positive angle with the horizontal axis (this means that curve is increasing from left to right).
- Negative if the line tangent at the curve at that point has a negative angle with the horizontal axis (this means that the curve is decreasing from left to right).
- Zero if the line tangent at the curve at that point is parallel to the horizontal axis (this means that the curve is remaining constant, has an inflection point or has reached a local maximum or minimum point).
The
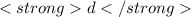 curve has a steady decreasing rate when
curve has a steady decreasing rate when
 is close zero and has one local maximum and one local minimum where the slope of the tangent line should be zero. The
is close zero and has one local maximum and one local minimum where the slope of the tangent line should be zero. The
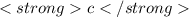 curve shows this behaviour so we can say that
curve shows this behaviour so we can say that
 is the derivative of
is the derivative of
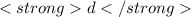 .
.
The
 curve reach a minimum point when
curve reach a minimum point when
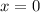 so the derivative should be zero at that point, with a decrasing rate for
so the derivative should be zero at that point, with a decrasing rate for
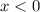 (negative derivative) and an increasing rate for
(negative derivative) and an increasing rate for
 (positive derivative). The
(positive derivative). The
 curve shows this behaviour so we can say that
curve shows this behaviour so we can say that
 is the derivative of
is the derivative of
 .
.
The
 curve is constantly increasing, so its derivative is going to be always positive and has an inflection point in
curve is constantly increasing, so its derivative is going to be always positive and has an inflection point in
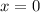 where the slope of the tangent line should be zero, then
where the slope of the tangent line should be zero, then
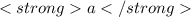 is the derivative of
is the derivative of

Recapitulating:
 is the derivative of
is the derivative of

 is the derivative of
is the derivative of

 is the derivative of
is the derivative of

Then:
f --> d
f' --> c
f'' --> b
f''' --> a